Обычно отношение эквивалентности обозначают знаком
Определение 8
. Отношение
называется отношением эквивалентности, если оно обладает следующими свойствами:
(рефлексивность)
- Если
(симметричность)
- Если
, то 
и говорят, что оно (отношение) задано на множестве 
). Условия 1-3 в таких обозначениях выглядят более естественно:
(рефлексивность)
- Если
(симметричность)
- Если
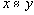
, то 
разбивается на взаимно непересекающиеся подмножества, состоящие из эквивалентных друг другу элементов (классы эквивалентности).
Определение 8
. Соединением отношений
по условию 
и 
Таким образом, операция соединения есть результат последовательного применения операций декартового произведения и выборки. Если в отношениях 
имеются атрибуты с одинаковыми наименованиями, то перед выполнением соединения такие атрибуты необходимо переименовать.
пятой нормальной форме (5НФ) тогда и только тогда, когда любая имеющаяся зависимость соединения является тривиальной.
Определения 5НФ может стать более понятным, если сформулировать его в отрицательной форме:
